Authors:
(1) Rafael Rafailo, Stanford University and Equal contribution; more junior authors listed earlier;
(2) Archit Sharma, Stanford University and Equal contribution; more junior authors listed earlier;
(3) Eric Mitchel, Stanford University and Equal contribution; more junior authors listed earlier;
(4) Stefano Ermon, CZ Biohub;
(5) Christopher D. Manning, Stanford University;
(6) Chelsea Finn, Stanford University.
Table of Links
4 Direct Preference Optimization
7 Discussion, Acknowledgements, and References
A Mathematical Derivations
A.1 Deriving the Optimum of the KL-Constrained Reward Maximization Objective
A.2 Deriving the DPO Objective Under the Bradley-Terry Model
A.3 Deriving the DPO Objective Under the Plackett-Luce Model
A.4 Deriving the Gradient of the DPO Objective and A.5 Proof of Lemma 1 and 2
B DPO Implementation Details and Hyperparameters
C Further Details on the Experimental Set-Up and C.1 IMDb Sentiment Experiment and Baseline Details
C.2 GPT-4 prompts for computing summarization and dialogue win rates
D Additional Empirical Results
D.1 Performance of Best of N baseline for Various N and D.2 Sample Responses and GPT-4 Judgments
4 Direct Preference Optimization
Motivated by the challenges of applying reinforcement learning algorithms on large-scale problems such as fine-tuning language models, our goal is to derive a simple approach for policy optimization using preferences directly. Unlike prior RLHF methods, which learn a reward and then optimize it via RL, our approach leverages a particular choice of reward model parameterization that enables extraction of its optimal policy in closed form, without an RL training loop. As we will describe next in detail, our key insight is to leverage an analytical mapping from reward functions to optimal policies, which enables us to transform a loss function over reward functions into a loss function over policies. This change-of-variables approach avoids fitting an explicit, standalone reward model, while still optimizing under existing models of human preferences, such as the Bradley-Terry model. In essence, the policy network represents both the language model and the (implicit) reward.
Deriving the DPO objective. We start with the same RL objective as prior work, Eq. 3, under a general reward function r. Following prior work [29, 28, 17, 15], it is straightforward to show that the optimal solution to the KL-constrained reward maximization objective in Eq. 3 takes the form:

The derivation is in Appendix A.2. While Eq. 6 uses the Bradley-Terry model, we can similarly derive expressions under the more general Plackett-Luce models [30, 21], shown in Appendix A.3.
Now that we have the probability of human preference data in terms of the optimal policy rather than the reward model, we can formulate a maximum likelihood objective for a parametrized policy πθ. Analogous to the reward modeling approach (i.e. Eq. 2), our policy objective becomes:
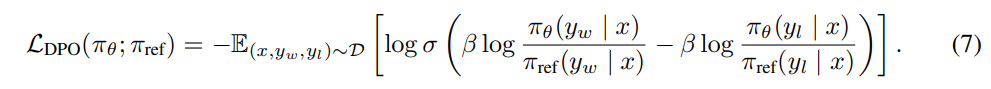
This way, we fit an implicit reward using an alternative parameterization, whose optimal policy is simply πθ. Moreover, since our procedure is equivalent to fitting a reparametrized Bradley-Terry model, it enjoys certain theoretical properties, such as consistencies under suitable assumption of the preference data distribution [4]. In Section 5, we further discuss theoretical properties of DPO in relation to other works.

This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.

