Authors:
(1) Rafael Rafailo, Stanford University and Equal contribution; more junior authors listed earlier;
(2) Archit Sharma, Stanford University and Equal contribution; more junior authors listed earlier;
(3) Eric Mitchel, Stanford University and Equal contribution; more junior authors listed earlier;
(4) Stefano Ermon, CZ Biohub;
(5) Christopher D. Manning, Stanford University;
(6) Chelsea Finn, Stanford University.
Table of Links
4 Direct Preference Optimization
7 Discussion, Acknowledgements, and References
A Mathematical Derivations
A.1 Deriving the Optimum of the KL-Constrained Reward Maximization Objective
A.2 Deriving the DPO Objective Under the Bradley-Terry Model
A.3 Deriving the DPO Objective Under the Plackett-Luce Model
A.4 Deriving the Gradient of the DPO Objective and A.5 Proof of Lemma 1 and 2
B DPO Implementation Details and Hyperparameters
C Further Details on the Experimental Set-Up and C.1 IMDb Sentiment Experiment and Baseline Details
C.2 GPT-4 prompts for computing summarization and dialogue win rates
D Additional Empirical Results
D.1 Performance of Best of N baseline for Various N and D.2 Sample Responses and GPT-4 Judgments
A.4 Deriving the Gradient of the DPO Objective
In this section we derive the gradient of the DPO objective:
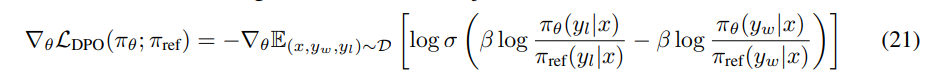
We can rewrite the RHS of Equation 21 as
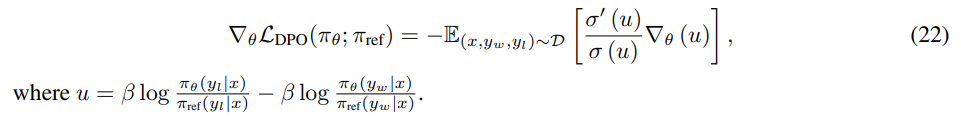
Using the properties of sigmoid function σ ′ (x) = σ(x)(1 − σ(x)) and σ(−x) = 1 − σ(x), we obtain the final gradient
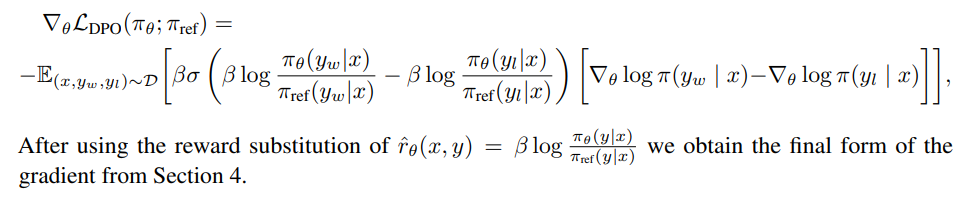
A.5 Proof of Lemma 1 and 2
In this section, we will prove the two lemmas from Section 5.
Lemma 1 Restated. Under the Plackett-Luce preference framework, and in particular the Bradley-Terry framework, two reward functions from the same equivalence class induce the same preference distribution.

which completes the proof.
Lemma 2 Restated. Two reward functions from the same equivalence class induce the same optimal policy under the constrained RL problem.

which completes the proof.
This paper is available on arxiv under CC BY-NC-ND 4.0 DEED license.

