Authors:
(1) Seokil Ham, KAIST;
(2) Jungwuk Park, KAIST;
(3) Dong-Jun Han, Purdue University;
(4) Jaekyun Moon, KAIST.
Table of Links
3. Proposed NEO-KD Algorithm and 3.1 Problem Setup: Adversarial Training in Multi-Exit Networks
4. Experiments and 4.1 Experimental Setup
4.2. Main Experimental Results
4.3. Ablation Studies and Discussions
5. Conclusion, Acknowledgement and References
B. Clean Test Accuracy and C. Adversarial Training via Average Attack
E. Discussions on Performance Degradation at Later Exits
F. Comparison with Recent Defense Methods for Single-Exit Networks
G. Comparison with SKD and ARD and H. Implementations of Stronger Attacker Algorithms
A Experiment Details
We provide additional implementation details that were not described in the main manuscript.
A.1 Model training

A.2 Adversarial training

Additionally, the hyperparameter α for NKD is set to 3, and β for EOKD is set to 1 across all experiments. On the other hand, the exit-balancing parameter γ is set to [1, 1, 1] for MNIST and CIFAR-10, and [1, 1, 1, 1.5, 1.5], [1, 1, 1, 1.5, 1.5, 1.5, 1.5] for Tiny-ImageNet/ImageNet, CIFAR-100, respectively.
A.3 How to determine confidence threshold in budgeted prediction setup
We provide a detailed explanation about how to determine confidence threshold for each exit using validation set before the testing phase. First, in order to obtain confidence thresholds for various budget scenarios, we allocate the number of validation samples for each exit. For simplicity, consider a toy example with 3-exit network (i.e., L = 3) and assume the number of validation set is 3000. Then, each exit can be assigned a different number of samples: for instance, (2000, 500, 500), (1000, 1000, 1000) and (500, 1000, 1500). As more samples are allocated to the early exits, a scenario with a smaller budget can be obtained, while allocating more data to the later exits can lead to a scenario with a larger budget. More specifically, to see how to obtain the confidence threshold for each exit, consider the low-budget case of (2000, 500, 500). The model first makes predictions on all 3000 samples at exit 1 and sorts the samples based on their confidence. Then, the 2000-th largest confidence value is set as the confidence threshold for the exit 1. Likewise, the model performs predictions on remaining 1000 samples at exit 2 and the 500-th largest confidence is determined as the threshold for exit 2. Following this process, all thresholds for each exit are determined. During the testing phase, we perform predictions on test samples based on the predefined thresholds for each exit, and calculate the total computational budget for the combination of (2000, 500, 500). In this way, we can obtain accuracy and computational budget for different combinations of data numbers
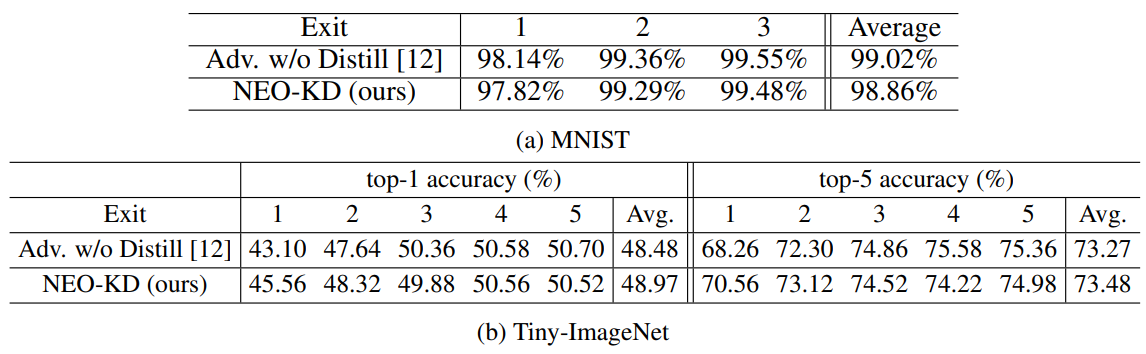
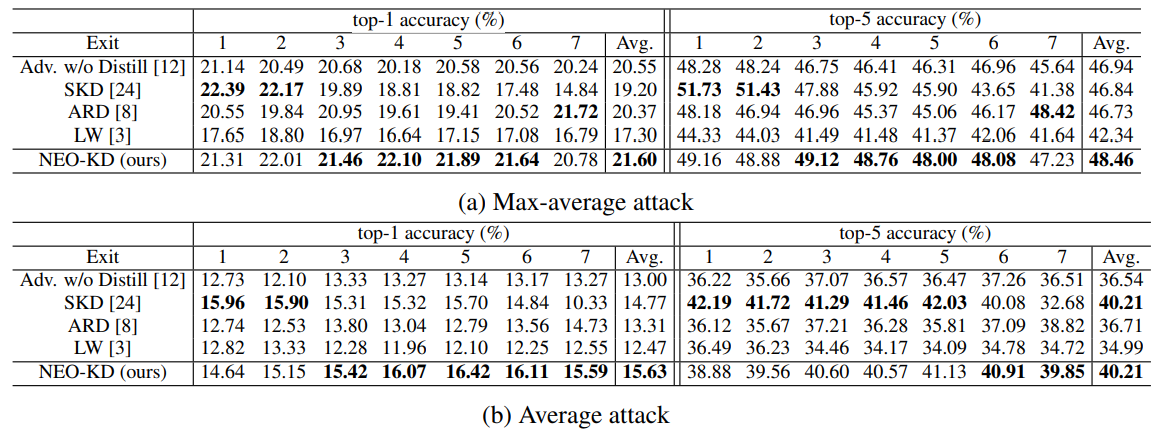
(i.e., various budget scenarios). Figures 2 and 3 in the main manuscript show the results for 100 cases of different budget scenarios.
This paper is available on arxiv under CC 4.0 license.
[2] https://github.com/VITA-Group/triple-wins
[3] https://github.com/kalviny/MSDNet-PyTorch

