Authors:
(1) Wahei Hara;
(2) Yuki Hirano.
Table of Links
- Abstract and Intro
- Exchanges and Mutations of modifying modules
- Quasi-symmetric representation and GIT quotient
- Main results
- Applications to Calabi-Yau complete intersections
- Appendix A. Matrix factorizations
- Appendix B. List of Notation
- References

1. Introduction
1.1. Backgrounds. A crepant resolution is one of the best modifications of singularities. This can be regarded as a higher dimensional analog of minimal resolutions of surface singularities, and in the terminology from minimal model theory, a crepant resolution can be paraphrased as a smooth minimal model of the singularity.
As a noncommutative analog of the notion of crepant resolutions, Van den Bergh introduced noncommutative crepant resolutions (= NCCRs) [Van2, Van3]. In both commutative and noncommutative cases, the existence of such a resolution is not always true. There are two large classes of singularities for which the study of NCCRs (and crepant resolutions) is well established. One is the class of quotient singularities arising from quasi-symmetric representations of reductive groups, which was first studied in [SV1], and the other is the class of (3-fold) compound du Val singularities, studied in [Van1, Wem]. To investigate the latter class, Iyama and Wemyss [IW1] introduced an operation called mutation, which produce a new NCCR from the original one. By Kawamata [Kaw], it is known that all minimal models (and hence all crepant resolutions) are connected by iterated flops, and mutations can be regarded as a noncommutative counterpart of flops. Indeed, it is proved in [Wem] that the derived equivalences associated to 3-fold flops, which are established in [Bri, Che], correspond to derived equivalences associated to mutations of NCCRs. This interpretation and the technique of mutations of NCCRs provides the main ingredients for the study of Bridgeland stability conditions for 3-fold flops [HW1, HW2].
The main purpose of this paper is to import such a technology established by [IW1] to deepen the study of NCCRs for quotient singularities arising from quasi-symmetric representations, by studying the combinatorics associated to the representation, and by accessing to the ideas from [HSa, SV1].
1.2. Exchanges and mutations of modifying modules. The present section, Section 1.3, and Section 1.4 explain the setting of this paper, and recall some terminologies, notations, and known results that are needed to state our results. The precise statements of main results are given in Section 1.5.
Let R be a normal equidimensional Gorenstein ring. A finitely generated reflexive Rmodule M is said to be modifying if the endomorphism ring EndR(M) is Cohen-Macaulay as an R-module. A noncommutative crepant resolution (=NCCR) of R is the endomorphism ring Λ = EndR(M) of some modifying R-module M such that the global dimension of Λ is finite. If EndR(M) is an NCCR, we say that M gives an NCCR. The following is one of the central problems about NCCRs.
Conjecture 1.1 ([Van2]). Let R be an equidimensional normal Gorenstein ring. Then all crepant resolutions and all NCCRs of R are derived equivalent. In relation to this derived equivalence problem, Iyama and Wemys

It is natural to ask if two given NCCRs are connected by (iterated) mutations or not. It is known that, for many types of singularities, their natural NCCRs are actually connected by mutations [Har1, Har2, HN, Nak, SV5, Wem]. One of the main aims of this paper is to present a similar result for NCCRs associated to the quotient of quasi-symmetric representations, which are recalled in the next section.


will be constructed, and using this yields
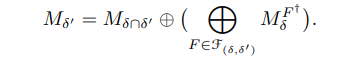
The following is our main result.


Acknowledgements. W. H. would like to thank Prof. Michael Wemyss for discussions and comments. W. H. was supported by EPSRC grant EP/R034826/1 and by ERC Consolidator Grant 101001227 (MMiMMa). Y. H. was supported by JSPS KAKENHI 19K14502.
This paper is available on arxiv under CC0 1.0 DEED license.
