Authors:
(1) Seokil Ham, KAIST;
(2) Jungwuk Park, KAIST;
(3) Dong-Jun Han, Purdue University;
(4) Jaekyun Moon, KAIST.
Table of Links
3. Proposed NEO-KD Algorithm and 3.1 Problem Setup: Adversarial Training in Multi-Exit Networks
4. Experiments and 4.1 Experimental Setup
4.2. Main Experimental Results
4.3. Ablation Studies and Discussions
5. Conclusion, Acknowledgement and References
B. Clean Test Accuracy and C. Adversarial Training via Average Attack
E. Discussions on Performance Degradation at Later Exits
F. Comparison with Recent Defense Methods for Single-Exit Networks
G. Comparison with SKD and ARD and H. Implementations of Stronger Attacker Algorithms
3.2 Algorithm Description
To tackle the limitations of prior works [3, 12], we propose neighbor exit-wise orthogonal knowledge distillation (NEO-KD), a self-distillation strategy tailored to robust multi-exit networks. To gain insights, we divide our solution into two distinct components with different roles - neighbor knowledge distillation and exit-wise orthogonal knowledge distillation - and first describe each component separately, and then put together into the overall NEO-KD method. A high-level description of our approach is given in Figure 1.
Neighbor knowledge distillation (NKD). The first component of our solution, NKD, guides the output feature of adversarial data at each exit to mimic the output feature of clean data. Specifically, the proposed NKD loss of the j-th train sample at the i-th exit is written as follows:
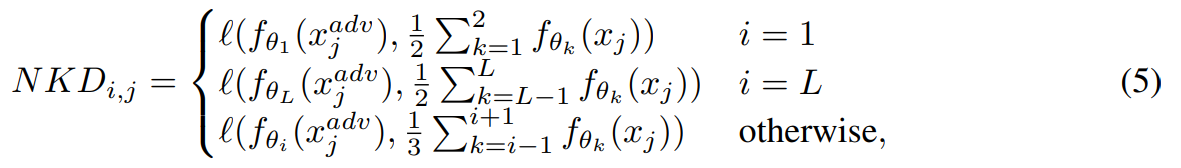
which can be visualized with the colored arrows as in Figure 1a. Different from previous self-knowledge distillation methods, for each exit i, NKD generates a teacher prediction by ensembling (averaging) the neighbor predictions (i.e., from exit i − 1 and exit i + 1) of clean data and distills it to each prediction of adversarial examples.
Compared to other distillation strategies, NKD takes advantage of only these neighbors during distillation, which has the following key advantages for improving adversarial robustness. First, by ensembling the neighbor predictions of clean data before distillation, NKD provides a higher quality feature of the original data to the corresponding exit; compared to the naive baseline that is distilled with only one exit in the same position (without ensembling), NKD achieves better adversarial accuracy, where the results are provided in Table 7. Secondly, by considering only the neighbors during ensembling, we can distill different teacher predictions to each exit. Different teacher predictions of NKD also play a role of reducing adversarial transferability compared to the strategies that distill the same prediction (e.g., the last exit) to all exit; ensembling other exits (beyond the neighbors) increases the dependencies among submodels, resulting in higher adversarial transferability. The corresponding results are also shown via experiments in Section 4.3.
However, a multi-exit network trained with only NKD loss still has a significant room for mitigating adversarial transferability further. In the following, we describe the second part of our solution that solely focuses on reducing adversarial transferability of multi-exit networks.
Exit-wise orthogonal knowledge distillation (EOKD). EOKD provides orthogonal soft labels to each exit for the non-ground-truth predictions, in an exit-wise manner. As can be seen from the red arrows in Figure 1b, the output of clean data at the i-th exit is distilled to the output of adversarial example at the i-th exit. During this exit-wise distillation process, some predictions are discarded to encourage the non-ground-truth predictions of individual exits to be mutually orthogonal. We randomly allocate the classes of non-ground-truth predictions to each exit for every epoch, which prevents the classifier to be biased compared to the fixed allocation strategy. The proposed EOKD loss of the j-th sample at the i-th exit is defined as follows:

Overall NEO-KD loss. Finally, considering the proposed loss functions in Eq. (5), (6) and the original adversarial training loss, the overall objective function of our scheme is written as follows:
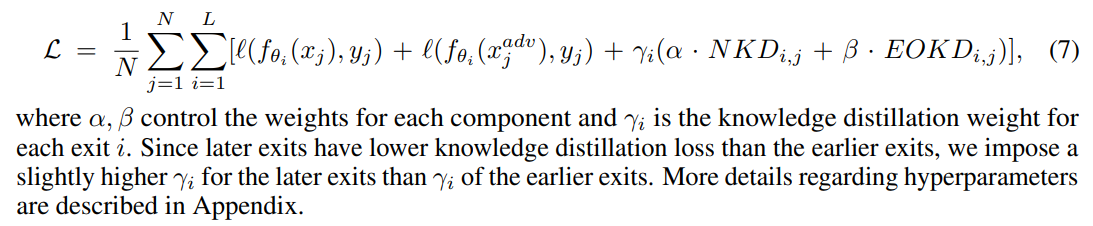
By introducing two unique components - NKD and EOKD - the overall NEO-KD loss function in Eq. (7) reduces adversarial transferability in the multi-exit network while correctly guiding the output of the adversarial examples in each exit, significantly improving the adversarial robustness of multi-exit networks, as we will see in the next section.
This paper is available on arxiv under CC 4.0 license.

