Author:
(1) Brandon T. Willard, Normal Computing;
(2) R´emi Louf, Normal Computing.
Table of Links
- Abstract and Intro
- LLM Sampling and Guided Generation
- Iterative FSM Processing and Indexing
- Extensions to Iterative Parsing
- Discussion, References and Acknowledgments
2. LLM Sampling and Guided Generation
Let St = (s1 . . . st) represent a sequence of t tokens with st ∈ V, V a vocabulary, and |V| = N. The vocabularies, V, are composed of strings from a fixed alphabet [Sennrich et al., 2015] and N is often on the order of 104 or larger.
We define the next token st+1 as the following random variable:
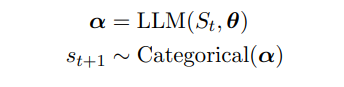

2.1 Sampling sequences
Let F ⊂ P (V), where P is the powerset operator, be subsets of multi-token strings that end with a special token EOS ∈ V. The text generation task is to draw samples from F.
Several procedures have been considered to generate elements of F. Greedy decoding consists in generating tokens recursively, choosing the token with highest probability at each step. Beam search also generates tokens recursively, using a heuristic to find the mode of the distribution. More recently, SMC sampling has also been used to generate sequences [Lew et al., 2023].

The sampling procedure is described in generality by Algorithm 1. Often called multinomial sampling, the procedure recursively generates new tokens by sampling from the categorical distribution defined above until the EOS token is found.
2.2 Guiding generation

• digit samples,
• strings that match the regular expression [a-zA-Z],
• and strings that parse according to a specified grammar (e.g. Python, SQL, etc.)
The sampling procedure with masking is a simple augmentation of Algorithm 1 and is provided in Algorithm 2.
The computation of m on line 2.5 is implicitly performed over all the elements of V. Aside from computing α, this step is easily the most expensive. In the case of regular expression-guided masking–and cases more sophisticated than that–the support and, thus, m will necessarily depend on the previously sampled tokens. Guided generation of this kind is ultimately an iterative matching or parsing problem and is not directly amenable to standard approaches that require access to a complete string upfront. In some cases, partial matching or parsing can be performed from the start of the sampled sequence on each iteration, but this has a cost that grows at least linearly alongside the O(N) cost of its application across the entire vocabulary.
This leads us to the main questions of this work: how can we efficiently match or parse incomplete strings according to a regular expression or CFG and determine the masks m at each iteration of Algorithm 2?

This paper is available on arxiv under CC 4.0 license.

