This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.
Authors:
(1) Ke Hong, Tsinghua University & Infinigence-AI;
(2) Guohao Dai, Shanghai Jiao Tong University & Infinigence-AI;
(3) Jiaming Xu, Shanghai Jiao Tong University & Infinigence-AI;
(4) Qiuli Mao, Tsinghua University & Infinigence-AI;
(5) Xiuhong Li, Peking University;
(6) Jun Liu, Shanghai Jiao Tong University & Infinigence-AI;
(7) Kangdi Chen, Infinigence-AI;
(8) Yuhan Dong, Tsinghua University;
(9) Yu Wang, Tsinghua University.
Table of Links
- Abstract & Introduction
- Backgrounds
- Asynchronized Softmax with Unified Maximum Value
- Flat GEMM Optimization with Double Buffering
- Heuristic Dataflow with Hardware Resource Adaption
- Evaluation
- Related Works
- Conclusion & References
ABSTRACT
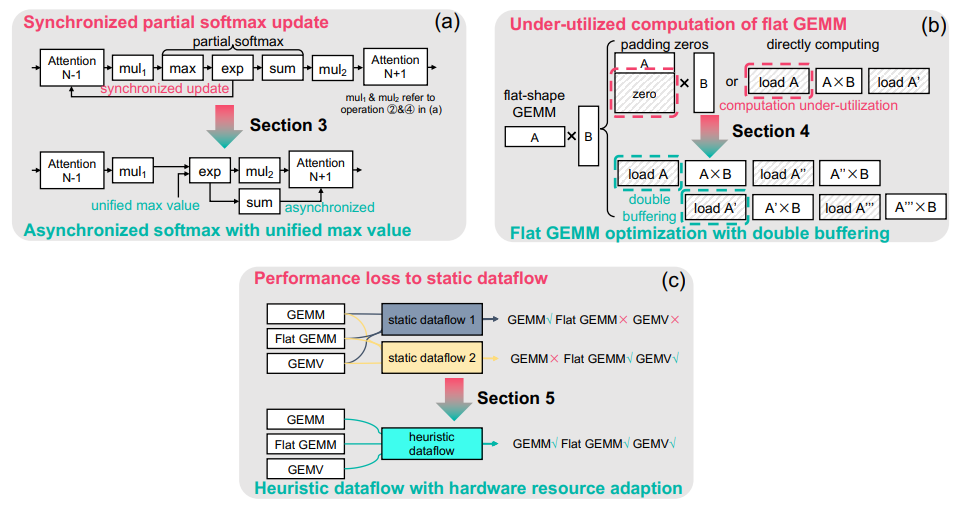
As the Large Language Model (LLM) becomes increasingly important in various domains, the performance of LLM inference is crucial to massive LLM applications. However, the following challenges still remain unsolved in accelerating LLM inference: (1) Synchronized partial softmax update. The softmax operation requires a synchronized update operation among each partial softmax result, leading to ∼20% overheads for the attention computation in LLMs. (2) Under-utilized computation of flat GEMM. The shape of matrices performing GEMM in LLM inference is flat, leading to under-utilized computation and >50% performance loss after padding zeros in previous designs (e.g., cuBLAS, CUTLASS, etc.). (3) Performance loss due to static dataflow. Kernel performance in LLM depends on varied input data features, hardware configurations, etc. A single and static dataflow may lead to a 50.25% performance loss for GEMMs of different shapes in LLM inference.
We present FlashDecoding++, a fast LLM inference engine supporting mainstream LLMs and hardware back-ends. To tackle the above challenges, FlashDecoding++ creatively proposes: (1) Asynchronized softmax with unified max value. FlashDecoding++ introduces a unified max value technique for different partial softmax computations to avoid synchronization. Based on this, the fine-grained pipelining is proposed.(2) Flat GEMM optimization with double buffering. FlashDecoding++ points out that flat GEMMs with different shapes face varied bottlenecks. Then, techniques like double buffering are introduced. (3) Heuristic dataflow with hardware resource adaptation. FlashDecoding++ heuristically optimizes dataflow using different hardware resource (e.g., Tensor Core or CUDA core) considering input dynamics.Due to the versatility of optimizations in FlashDecoding++, FlashDecoding++ can achieve up to 4.86× and 2.18× speedup on both NVIDIA and AMD GPUs compared to Hugging Face implementations. FlashDecoding++ also achieves an average speedup of 1.37× compared to state-of-the-art LLM inference engines on mainstream LLMs.
1 Introduction
As the Large Language Model (LLM) achieved unprecedented success in various domains [2, 3, 4, 5], the LLM inference workload is skyrocketing. For example, OpenAI reports that GPT-4 inference with 8K context length costs $0.03 per 1K input tokens and $0.06 per 1K output tokens [6]. Currently, OpenAI has 180.5 million users and receives over 10 million queries per day [7]. Consequently, the cost to operate OpenAI’s model like ChatGPT is approximately $7 million per day for the necessary computing hardware [8]. Thus, optimizations on LLM inference performance will have a huge impact considering massive LLM inference scenarios. Many recent works have proposed techniques to accelerate LLM inference tasks, including DeepSpeed [9], FlexGen [10], vLLM [11], OpenPPL [12], FlashDecoding [13], TensorRT-LLM [14], and etc [15, 16, 17, 12].
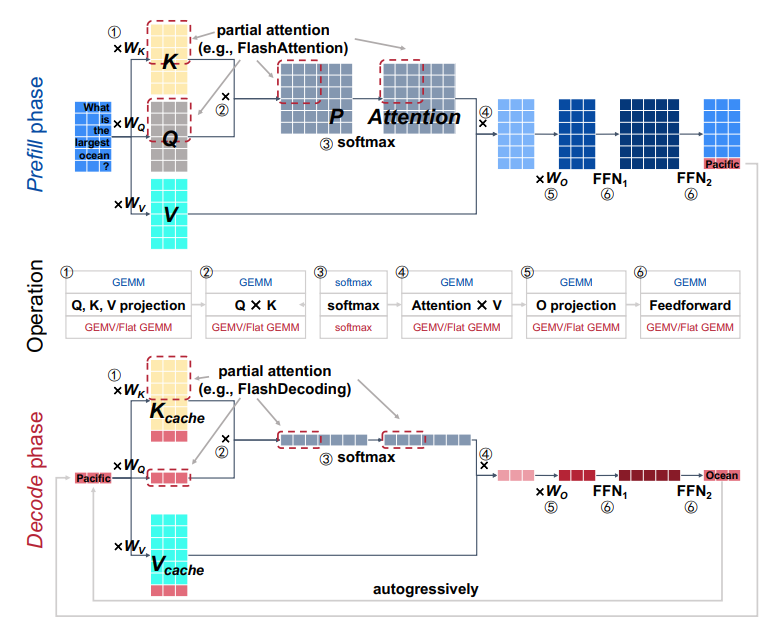
The LLM inference task generates tokens (e.g., words) from the input sequence autoregressively, and can be organized into two typical phases: the prefill phase and the decode phase. The prefill phase generates the first token by processing the input prompt, and previous research (e.g., FlashAttention [18, 19]) optimizes latency for this phase. The decode phase generates the following tokens sequentially, and many works [9, 10, 11, 15, 13, 14, 20] focus on improving the throughput of generating tokens (i.e., reducing latency of each token). The prefill phase dominates total time for scenarios of long-sequence input or generating short outputs [21, 22], while the decode phase constitutes a significant portion of the time when processing long output sequences [23].
Figure 2 shows the main dataflow of the LLM inference with one transformer layer for both the prefill phase and the decode phase. A transformer layer can be divided into linear GEMM (General Matrix Multiplication) operations (e.g., K, Q, V, O weight projection and the feedforward) and the attention/softmax computation. For the attention computation, a softmax operation is adopted for a row in the attention matrix. To improve the parallelism, previous designs [18, 13] divide the attention matrices into smaller tiles and rows are also split to compute partial softmax results. A synchronized softmax operation is adopted to update previous partial softmax results when a new partial softmax result is calculated. Such a synchronized partial softmax update accounts for 18.8% for the attention computation of Llama2-7B inference according to our profiling on NVIDIA Tesla A100 GPU with 1024 input length, resulting in the first challenge for accelerating LLM inference. Secondly, the computation resources is under-utilized for the flat GEMM operation during the decode phase. Because the decode phase sequentially generates tokens, the linear GEMM operation tends to be flat-shape (even turning into the GEMV (General Matrix-Vector Multiplication) operation when the batch size is 1). For the small batch size (e.g., 8), previous designs [24, 25] pad the matrix with zeros to perform GEMMs of larger sizes (e.g., 64), leading to over 50% computation under-utilization. Thirdly, the performance of LLM inference suffers from the static dataflow considering input dynamics and hardware configuration. For example, the small batch size makes the decode phase of LLM inference memory-bounded and the large batch size makes it compute-bounded. A single and static dataflow may lead to 50.25% performance loss for GEMMs of different shapes in LLM inference.
![Figure 1: Overview of comparison between FlashDecoding++ and state-of-the-art designs. The results in the figure are reported with Llama2-7B model [1]. The left is with batch size=1 and input length=1K, and TensorRT-LLM and Hugging Face are the SOTA baseline for NVIDIA/AMD according to our experimental results. The right shows the comprehensive comparison of both first token latency and each token latency.](https://cdn.hackernoon.com/images/fWZa4tUiBGemnqQfBGgCPf9594N2-a983uuk.png)
To tackle these challenges and enable a faster Large Language Model (LLM) inference, we present FlashDecoding++ in this paper. FlashDecoding++ creatively proposes the following contributions:
• Asynchronized softmax with unified max value. FlashDecoding++ leverages a unified max value for different partial softmax computations. Each partial softmax result can be processed individually without synchronized update.
• Flat GEMM optimization with double buffering. FlashDecoding++ only pads the matrix size to 8 rather than 64 in previous designs for flat-shaped GEMM to improve computation utilization. We point out that flat GEMMs with different shapes face varied bottlenecks, and further improve the kernel performance with techniques like double buffering.
• Heuristic dataflow with hardware resource adaption. FlashDecoding++ takes both input dynamics and hardware configurations into consideration and dynamically applies kernel optimization for the LLM inference dataflow.
Because of the versatility of optimizations, the effectiveness of FlashDecoding++ can be proved on both NVIDIA and AMD GPUs. FlashDecoding++ achieves up to 4.86× and 2.18× speedup on both NVIDIA and AMD GPUs compared with Hugging Face implementations, respectively. Our extensive results show that FlashDecoding++ achieves an average of 1.37× speedup compared with FlashDecoding [13], a state-of-the-art LLM inference engine on various LLMs (e.g., Llama2, ChatGLM2, etc.).
The rest of this paper is organized as follows. Section 2 introduces preliminaries of LLMs and related works on LLM inference acceleration. Our three techniques, the asynchronized softmax with unified max value, the flat GEMM optimization with double buffering, and the heuristic dataflow with hardware resource adaption are detailed in Section 3, 4, and 5, respectively. Section 6 presents the evaluation results. Related works on LLM inference are introduced in Section 7, and Section 8 concludes the paper.