This paper is available on arxiv under CC BY-NC-SA 4.0 DEED license.
Authors:
(1) Ke Hong, Tsinghua University & Infinigence-AI;
(2) Guohao Dai, Shanghai Jiao Tong University & Infinigence-AI;
(3) Jiaming Xu, Shanghai Jiao Tong University & Infinigence-AI;
(4) Qiuli Mao, Tsinghua University & Infinigence-AI;
(5) Xiuhong Li, Peking University;
(6) Jun Liu, Shanghai Jiao Tong University & Infinigence-AI;
(7) Kangdi Chen, Infinigence-AI;
(8) Yuhan Dong, Tsinghua University;
(9) Yu Wang, Tsinghua University.
Table of Links
- Abstract & Introduction
- Backgrounds
- Asynchronized Softmax with Unified Maximum Value
- Flat GEMM Optimization with Double Buffering
- Heuristic Dataflow with Hardware Resource Adaption
- Evaluation
- Related Works
- Conclusion & References
3 Asynchronized Softmax with Unified Maximum Value
Motivation. The partial softmax operation requires synchronization among different partial vectors, leading to ∼20% overheads of the attention operation. As is shown in Figure 2, the synchronization is required after the maximum value of the partial vector is calculated. The maximum value is used to update previous partial softmax (i.e., recompute previous attention) results. Thus, to reduce synchronization overheads, the key problem to be solved is how to compute each partial softmax result without requiring results from other partial softmax computation.
Challenge. The reason that synchronization is required lies in that the maximum value of each partial vector is different. The maximum value is used to avoid overflow of the exponent operation (f(x) in Figure 4(a)), and exponents are summed (l(x) in Figure 4(a)) as the denominator of the softmax operation. Such a non-linear operation on each partial maximum value makes the synchronization among each partial softmax computation unavoidable.
Analysis and Insights. According to the formula of softmax computation, the maximum value is used as the scaling factor for both the numerator and the denominator (i.e., f(x) and l(x) in Figure 4(a)). Our key insight is, the scaling factor can be an arbitrary number rather than using the maximum value mathematically, shown in Equation (3). When we set ϕ = 0, it becomes the original softmax computation [30].
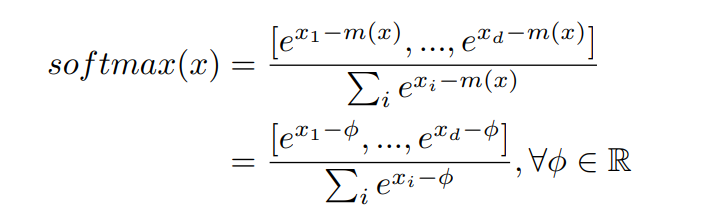
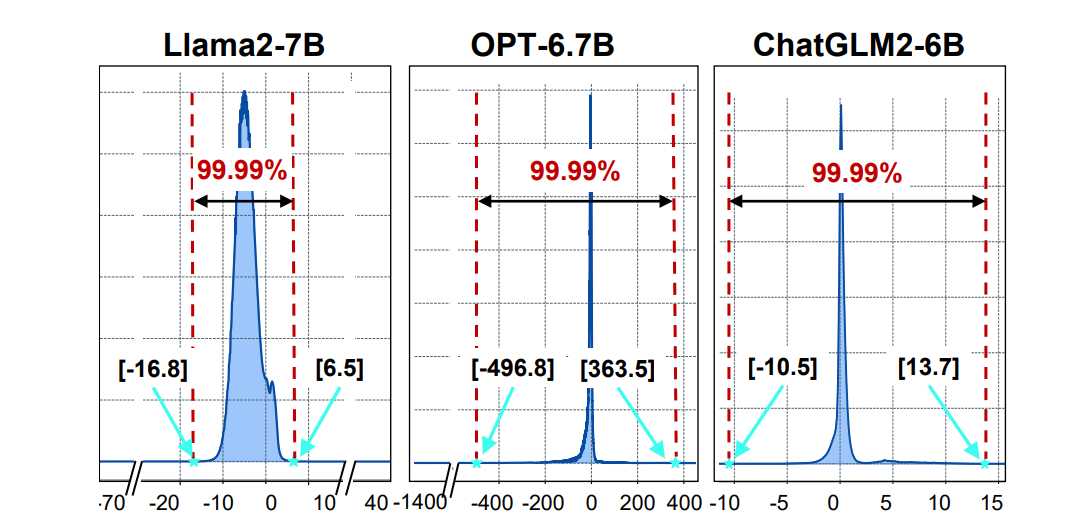
However, the scaling factor cannot be an arbitrary number considering the overflowing of the exponent computation. For the case where xi ≫ ϕ, e xi−ϕ overflows and cannot be represented using a fix-width floating point number (e.g., float32 for exponent results in current LLM engines). For another case where xi ≪ ϕ, e xi−ϕ → 0, leading to precision loss. Thus, a proper scaling factor ϕ should be carefully selected to avoid the two cases above. Figure 5 shows the statistical distribution of xi (elements in the input vectors of softmax) in typical LLMs with different inputs [31]. Our key insight is, > 99.99% xi are within a certain range. Specifically, for Llama2-7B, we have −16.8 < xi < 6.5 for > 99.99% xi . Because e b−a and e a−b can be represented by a float32 format, we can set ϕ = a in Equation (3). For OPT-6.7B, we do not apply the technique in this section because of the large range in Figure 5.
Approach: Asynchronization. Based on the insights above, each partial softmax computation shares a unified maximum value, ϕ. After the softmax operation, an inner product operation is executed between the softmax result and a column of V (i.e., v). Assume that the input vector x can be divided into p partial vectors, x = [x (1), ..., x(p) ] (v = [v (1), ..., v(p) ] correspondingly), we have:

The inner accumulation in both the numerator and the denominator only take the partial vectors x (j) and v (j) as input, thus they can be processed asynchronously and individually. The outer accumulation is only processed after all partial vectors are processed. As we can see in Figure 4(c), each f(x (j) ) is calculated individually, and sof tmax(x) is calculated after all x (j) is calculated.
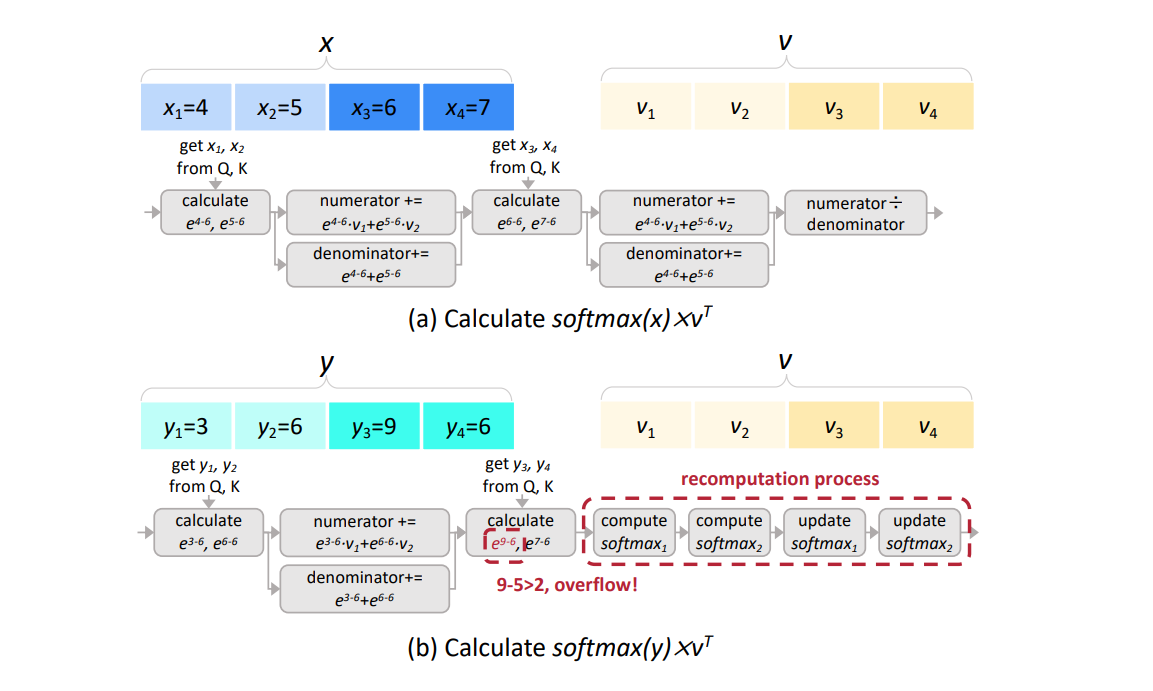
Approach: Recomputation. Without loss of generality, we assume a < xi − ϕ < b for each xi to ensure precision and avoid overflow. Then, the partial softmax operation is processed individually. However, when xi − ϕ ≤ a or xi − ϕ ≥ b, the asynchronized partial softmax computation is terminated for the vector x where xi belongs to. The softmax is then recomputed using the synchronized partial softmax scheme (used in FlashAttention [18, 19] and FlashDecoding [13]) shown in Figure 4(b). Such a recomputation scheme avoids overflow while introducing negligible overheads based on the statistical data shown in Figure 5.


